序文と目次の概要および補足を以下に示します．
鈴木登志雄「例題で学ぶ集合と論理」森北出版株式会社 (2016)
内容紹介
2024/10/16
定価2200円＋税．ISBN978-4-627-06191-0．菊判（A5より少しだけ大きい判），176ページ．
2016年1月29日発売． amazon（「試し読み」あり）， 楽天ブックス（「立ち読み機能」あり）， 紀伊國屋書店（「ためし読み」あり．電子版あり）， 森北出版（内容見本ＰＤＦあり）．
序文と目次の概要および補足を以下に示します．
序 その集合，ベン図で表せますか？ / 目次（概要） / 授業スケジュールの例 / 補足：用語の方言 / 補足：自習派のための板書写真 / 補足：発展的学習 / 別添資料 / 正誤表
（2022/ 1/ 1）第１版第１刷正誤表を改訂しました．先頭に②がある項目は第１版第２刷（2020年4月1日発行）に反映済みです．
（2020/12/07）別添資料「数え上げ」を掲載しました．有限集合の要素の個数，とくに数え上げにおける多項式の活用についての教材です．
（2018/11/12）別添資料「真理値表による命題論理の初歩」を掲載しました．第１章の自然演繹の部分を飛ばして，代わりに真理値表で命題論理にアプローチしたい人のための教材です．
読者のみなさんはベン図というものをご存じでしょう．二つの円周が横に並び，少し重なったおなじみの図です．ベン図は，要素と集合からなる２階建ての世界を表すのに向いています．たとえとして，水平方向には気の遠くなるほど長い２階建ての集合住宅を想像してください．１階には集合でないものたち，たとえば数やベクトルが住んでいます．２階にはものの集まりとしての集合が住んでいます．たとえば偶数全体の集合や，長さ１の平面ベクトル全体の集合などです．ベン図は，こういう世界を表すのに向いています．１階の住人を点で表し，２階の住人を円で表すのです．
ところが，大学の数学では同値関係と商集合という概念が必要不可欠であり，商集合は集合の集合です．つまり，大学では３階建てや４階建ての世界が必要であり，ベン図はこうした世界を表すのに向いていません．
本書は，大学の数学科１・２年生や，高校数学教職課程履修者を対象とした，集合と論理の教科書です．集合に重点をおいており，論理については集合の理解に必要な題材に絞り，あえて厳密な運用はしません．
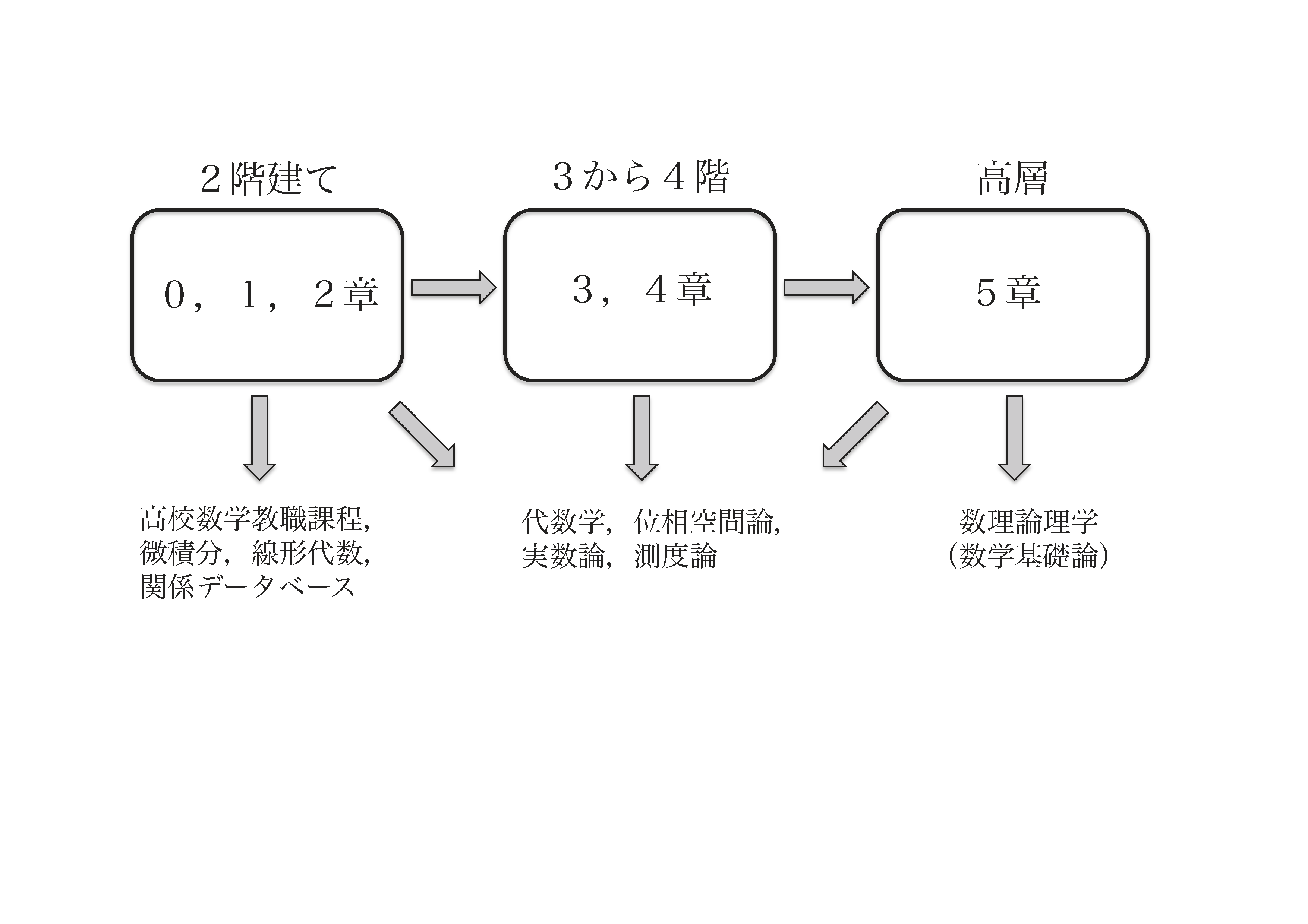
とくに，読者がベン図から無理なく自立していけるように，題材の配列を工夫してあります．ベン図を通して２階建ての世界を理解することから始まり（第０，１，２章），やがてベン図を少し裏切って３階建てや４階建ての世界へ行き（第３，４章），その後，高層建築の世界へ行ってベン図から巣立っていきます（第５章）．抽象的な事柄ほど後回しになっているので，大方の読者にとって，わかりやすい順の配列になっているはずです．
本書の構成
本書の構成は単純で，第３章までは一直線のストーリーです．第４章をとばして第５章を読むこともできます．
第０章では高校までの数学における集合と論理を復習するとともに，一段高いところから見渡し，その限界を理解します．第１章では大学レベルの話題のうち，とくに重要で基本的なものとして，命題論理の初歩，任意と存在，単射と全射を学びます．第２章では数学科の学生にとってとても大切な同値関係を学びます．
第３章では，ややとっつきにくいが面白い話題として集合族，べき集合，商集合，および濃度を学び，第４章では整列集合の初歩にふれます．
第５章では集合を用いて整数，有理数を再構成します．
第１章以降の各章末には，再確認用の公式集をつけています．章末問題は，やさしい順にＡ，Ｂ，Ｃにグループ分けしてあります．本文中の問いと章末問題すべてに対する解答を巻末に掲載しています．
本書で学ぶ内容と他分野の関係は，次の図のようになります．
授業をご担当の先生方へ
大学初年級「集合と論理」の教科書としておおむね標準的な内容を扱っています．
命題論理を導入する典型的なやり方には自然演繹，真理値表などいくつかありますが，本書は自然演繹を基にしています．このやり方を採用したおかげで，一時的な仮定を置く推論を正面から扱うことができました．背理法アレルギーを予防したい方のお役に立てれば幸いです．すでに背理法アレルギーになっている人が症状をこじらせないように，いくつかの箇所では，背理法を明示的には使わない証明と，明示的に使う証明を併記しています．
空写像は発展的学習として第２章の最後で扱っています．ここを飛ばしても後を読む上でほとんど影響はありません．
商集合をあえて第２章ではなく第３章に置いたのは教育的配慮によります．ベン図から離れられない人がつまずくのを先送りするためです．
謝辞
多くの方との対話を通じて，集合と論理について様々な見方があることを学びました．首都大学東京の同僚のみなさん，学生諸君，高大連携事業でお会いした都立高校の先生方，そして日本数学会の数学基礎論および歴史分科会の皆さんに感謝します．とくに日本大学理工学部数学科教授の志村立矢さんと法政大学文学部哲学科教授の安東祐希さんからは，本書の初期原稿にご感想を賜りました．ここに厚くお礼申し上げます．また，本書の企画と校正で大変お世話になった森北出版出版部の千先治樹さん，上村紗帆さんに感謝します．
第0章 高校までの復習と考察 （約30ページ）
（ 0.1 論理の一般常識， 0.2 集合と条件の一般常識， 0.3 中学校の論理と高校の集合・条件のつながり， 0.4 高校における道具立ての限界， 第０章の章末問題 ）
第1章 論理・集合・写像 （約40ページ）
（ 1.1 命題論理の初歩， 1.2 集合， 1.3 任意と存在， 1.4 「ならば」と部分集合， 1.5 関係と写像， 1.6 入れ子式の任意と存在， 1.7 記号についての補足， 第１章の公式集， 第１章の章末問題 ）
第2章 同値関係と順序関係 （約15ページ）
（ 2.1 直積と関係， 2.2 同値関係と代表元， 2.3 順序関係， 2.4 発展的学習 空写像， 第２章の公式集， 第２章の章末問題 ）
第3章 集合族と濃度 （約20ページ）
（ 3.1 べき集合と商集合， 3.2 濃度， 第３章の公式集， 第３章の章末問題 ）
第4章 整列集合 （約10ページ）
（ 4.1 「小なり」型の順序関係， 4.2 順序集合と同型写像， 4.3 整列集合， 第４章の公式集， 第４章の章末問題 ）
第5章 集合による数学概念の表現 （約15ページ）
（ 5.1 クラトウスキの順序対， 5.2 整数と有理数， 5.3 数列と添え字付き集合族， 5.4 フォンノイマンの順序数， 第５章の公式集， 第５章の章末問題 ）
補遺
問題解答・解説 （約20ページ）
あとがき・参考文献・索引
科目名としては「集合と論理」，「基礎数学」，通年科目「集合と位相」の前半部分などを想定しています．第１章の自然演繹の部分を飛ばして，代わりに真理値表で命題論理にアプローチしたい場合は別添資料「真理値表による命題論理の初歩」をご利用いただけます．
例１ 理学部 数学科あるいはそれに準じたコース，半期（1年次後期もしくは2年次前期），週1回90分
授業前：受講予定者は，授業が始まる前に第0章（高校までの復習と考察）および，第1章1.1節（命題論理の初歩）を読んでおくこと．
例２ 数学から離れた分野を学んでいる学科，半期，週1回90分
集合と論理にはいろいろな方言があります．本書は事典ではなく教科書なので，代表的な方言を網羅しているわけではありません．しかし，違う言葉づかいの本に出会って戸惑うことがあるかもしれません．ここに若干の補足を記します．
写像の相等についての方言
二つの写像が等しいということをどう定義するかについて，本書では集合論の言葉づかいにしたがっていますが，この他に，圏論の言葉づかいにしたがう流儀もあります．両者は以下のようになります．なお，写像 f:X→Y において，Yを終域といいます．
例 自然数全体の集合をN，整数全体の集合をZとする． NからNへの写像 f(x)=x+1と，NからZへの写像 g(x)=x+1を考える． （１）の意味では，fとgは等しい写像である．（２）の意味では，fとgは異なる写像である．
二つの流儀は一長一短です．
本書読了の後，圏論の本を読んで視野を広げてみるのもよいでしょう．
差集合についての方言
集合Aの要素のうち，集合Bに属さないものすべてからなる集まりを，AとBの差集合といいます．本書では A - B で表しています．
p.85，96，97で用いています．本文中に差集合の定義を書き忘れてしまい，すみませんでした．
文献によっては，AとBの差集合を A \ B で表すものもあります．
自習の場合も，仲間がいれば小さな段差は容易に乗り越えられます．しかし，近くに質問できる相手がいない人のために，板書の写真を掲載します．
差集合 (p.85，96，97)
定理3.1.1 集合Xからべき集合2Xへの写像fは全射でないこと．(p.91，対角線論法)
例として X={0,1,2}, f(0)={0,2}, f(1)={0}, f(2)={1,2} のときを考えます． fが全射でないことを示すためには，Xの部分集合Yで，f(0),f(1),f(2)のいずれとも違うものをがあることをいえばよいわけです．
まずホワイトボードのf(0)の行の，青い正方形（□）で囲った部分を見ます．0がf(0)に属することがわかります．そこで，0をYに入れないことにします．ホワイトボードのYの行を見ましょう．青い正方形（□）で囲った中には何も書いていません．0はf(0)に属すのにYには属さないから，f(0)とYが異なる集合であると保証できました．
まだYを定義する作業の途中なのに，青い正方形（□）で囲った部分だけで，f(0)とYが異なることを保証できたのが面白いところです．
次にホワイトボードのf(1)の行の，緑の正方形（□）で囲った部分を見ます．囲った部分の中には何も書いてありません．1がf(1)に属さないことがわかります．そこで，1をYに入れることにします．ホワイトボードのYの行を見ましょう．緑の正方形（□）で囲った中には1が書いてあります．1はf(1)に属さないのにYには属するから，f(1)とYが異なる集合であると保証できました．
緑の正方形（□）で囲った部分だけで，，f(1)とYが異なることを保証できましたね．
最後にホワイトボードのf(2)の行の，赤い正方形（□）で囲った部分を見ます．2がf(2)に属することがわかります．そこで，2をYに入れないことにします．ホワイトボードのYの行を見てください．赤の正方形（□）で囲った中に何も書いてありません．2はf(2)に属するのにYには属さないから，f(2)とYが異なる集合であると保証できました．
赤い正方形（□）で囲った部分だけで，f(2)とYが異なることを保証できました．
こうして，対角線の部分
□について考察することにより， Xの部分集合 Y={1} が，f(0),f(1),f(2)のいずれとも違うことがわかりました．
したがって，fはXからべき集合2Xへの全射ではありません．
上記のYは，よくみると集合 {x ∈ X | x ∉ f(x) } に他なりません．
例3.2.2 自然数全体の集合と整数全体の集合の濃度が等しいこと．(p.95)
f = f0 ∪ f1 として，整数 k を f(k)+1 番目に訪れることにしましょう．すると，蚊取り線香のようにぐるぐるまわって，すべての整数をもれなく１回ずつ訪れることができます．蚊取り線香をまっすぐ引き延ばせば，すべての整数を自然数と同じタイプの半直線上に並べることができます．これで，整数全体の集合が可算であることがわかりました．
蚊取り線香を知らない人は画像検索してください．想像の中でぐるぐるまわりたくない人は，Zの数直線を -1 と 0 の中点（よりも少し 0 に近い，数直線の -1/4 あたり）で折り返し，負の部分を正の部分に重ね置きしましょう．すると，
0,-1,1,-2,2,-3,3,-4,4,...
という並びができます．
定理3.2.2の証明の一部 開区間 (-π/2, π/2) と数直線の濃度が等しいこと．(p.99)
-π/2 より大きく π/2 未満の角度に，そのタンジェントを対応させるとは，どういうことでしょうか．単位円周上の，x座標が正の部分からなる半円に注目します．角度を決めると，半円上に点が決まります．原点から半円上のその点を通って伸びる直線が，直線 x=1 と交わる点のy座標が，もとの角度のタンジェントです．「なぜ？」と思った人へ：（この場合のタンジェント）=y/1=y．
本書を読み終えた人のために，発展的な内容を補足します．
集合とプロパークラスの違い
クラスには集合とプロパークラスがあります．
プロパークラスの例：すべての集合の集まり，すべての順序数の集まり，すべての基数の集まり，すべての順序集合の集まり，すべての群の集まり，すべての位相空間の集まり．
集合の例（１）：空集合，フォンノイマン自然数の各々．
集合論の公理は「どんなクラスが（プロパークラスではなく）集合になるか」を厳密に述べた約束事です．つまり，集合とプロパークラスをきちんと見分けるには公理的集合論を理解する必要があります．「なんだか理解に時間がかかりそうだな」と思うでしょう．たぶん，その通りです．
その一方，公理的集合論をほとんど知らなくても，大学２，３年レベルの代数・解析・幾何を理解する上で実害は少ないはずです．
そこで，一種の費用対効果に配慮して，本書では，あえて集合とプロパークラスの見分け方に言及していません．
巻末参考文献欄（p.155）の[4]，[7]が公理的集合論の入門書です．
「[4]，[7]は今の自分には難しすぎるけれど，あと一歩だけ先の景色を見せて」と思う人は，以下を読むのもよいでしょう．
[竹内2001] 竹内外史「新装版 集合とはなにか」講談社ブルーバックス (2001)
上記の本では，選択公理付きベルナイス・ゲーデル集合論（BGC）および，選択公理付きツェルメロ・フレンケル集合論（ZFC）の公理がどのようなものか，一般読書家向けに述べています．大雑把にいって，BGCとZFCは同じようなものであり，集合論の公理系として標準的なものです．以下に述べる「集合の例」とは，BGCにおいて（プロパークラスではなく）集合になるものの例です．
集合の例（２）：自然数の全体 ℕ，整数の全体 ℤ，有理数の全体 ℚ，実数の全体 ℝ，複素数の全体 ℂ
集合の例（３）：（A，Bが集合のとき）{ A, B }，和集合 A ∪ B，共通部分 A ∩ B，差集合 A - B，直積 A × B
集合の例（４）：（Aが集合族で，A自体も集合のとき）和集合 ∪ A
集合の例（５）：（Aが集合で，Fが写像のとき，ただしFはプロパークラスでもよい）FによるAの像 f[A]
集合の例（６）：（Aが集合のとき）Aの部分クラスの各々，Aのべき集合 2A
以下の解説記事は，ブルーバックス [竹内2001] と専門書 [4]，[7]の橋渡しになります．（検索するとダウンロードできるようです・・・）
[渕野2013] 渕野昌「公理的集合論--これから学ぶ人のために」『数学』岩波書店， 第65巻4号，pp.411--420 所収．
命題論理の「ならば」の感覚的理解についての補足
サブセクション1.1.8『命題論理の「ならば」の感覚的理解』を，少し違った手法で視覚化できます．余裕があれば以下の論文をご覧下さい．例0.2.2の図を発展させたものです．
Toshio Suzuki: "Visualization of set inclusion with gloves," CEUR Workshop Proceedings Vol-2116
(2018/11/12) 真理値表による命題論理の初歩『例題で学ぶ集合と論理』（森北出版，2016）非公式別添資料．
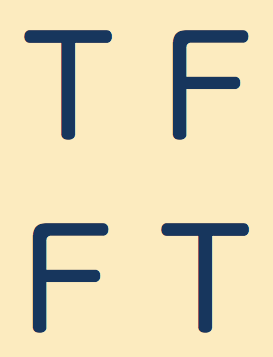第１章の自然演繹の部分を飛ばして，代わりに真理値表で命題論理にアプローチしたい人のための教材です．
(2020/12/ 7. タイプミス訂正版は2020/12/ 8) 数え上げ『例題で学ぶ集合と論理』（森北出版，2016）非公式別添資料．最初の版のタイプミス箇所を明示したものはこちらです．失礼しました．
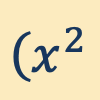有限集合の要素の個数，とくに数え上げにおける多項式の活用についての教材です．
(2019/ 9/25) 下線付き部分集合の記号はこの頃では用いられないのか
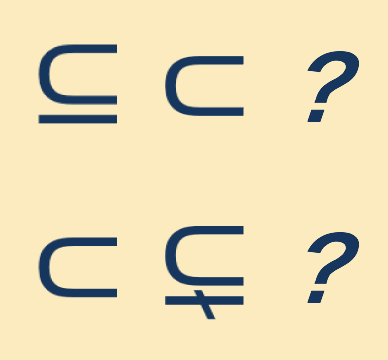部分集合の記号の方言についての話です．とくに『例題で学ぶ集合と論理』の別添資料というわけではありませんが，本書の読者にとっても興味深いと思うのでリンクを張っておきます．
第１版第１刷正誤表．2024年10月16日改訂．先頭に②がある項目は第１版第２刷（2020年4月1日発行）に反映済みです．
toshio-suzuki[at]tmu[dot]ac[dot]jp